9.1. Zadania

Zadanie 1

Rozkład łączny wektora losowego \((X, Y)\) podany jest w tabeli:

\(y_k\) \ \(x_n\)	0	2
-2	0.1	0.2
0	0	0.2
1	0.2	0.3

Wyznaczyć rozkłady brzegowe tego wektora losowego. Sprawdzić, czy zmienne losowe \(X\) i \(Y\) są niezależne.

Rozwiązanie

Należy sumować odpowiednie wiersze i kolumny w tabelce:

\(y_k\) \ \(x_n\)	0	2	\(p_{.k}\)
-2	0.1	0.2	0.3
0	0	0.2	0.2
1	0.2	0.3	0.5
\(p_{i.}\)	0.3	0.7	1

Zmienne nie są niezależne bo np. \(P(X=0, Y=0) = 0 \ne 0.6 = P(X=0)P(Y=0)\).

Zadanie 2

Dwuwymiarowa zmienna losowa \((X, Y)\) ma rozkład określony w tabelce:

\(y_k\) \ \(x_i\)	1	2	3
2	0.1	0.2	0.3
4	0.1	0.1	0.2

Wyznaczyć dystrybuantę rozkładu brzegowego zmiennej losowej \(Y\).

Rozwiązanie

Wyznaczę najpierw rozkład prawdopodobieństwa zmiennej \(Y\), trzeba tylko posumować wiersze z tabelki:

\(y_k\)	2	4
\(p_{.k}\)	0.6	0.4

Dystrybuantę wyznacza się teraz dla pojedynczej zmiennej losowej zgodnie ze wzorem nr (9) i jest to:

\(F_2(y) = \begin{cases} 0 & \text{dla } y \le 2, \\ 0.6 & \text{dla } 2 < y \le 4, \\ 1 & \text{dla } y > 4. \\ \end{cases}\)

Zadanie 3

Rozważmy dwie zmienne losowe \(X\) i \(Y\) których gęstość łączna przedstawiona jest w poniższej tabeli:

\(x_i\) \ \(y_k\)	0	1	2	\(p_{.k}\)
0	\(\frac{1}{6}\)	\(\frac{1}{4}\)	\(\frac{1}{8}\)	\(\frac{13}{24}\)
1	\(\frac{1}{8}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{11}{24}\)
\(p_{i.}\)	\(\frac{7}{24}\)	\(\frac{5}{12}\)	\(\frac{7}{24}\)	1

a) Oblicz \(P(X=0,Y \le 1)\).

b) Znajdź rozkłady brzegowe \(X\) i \(Y\).

c) Znajdź \(P(Y=1|X=0)\).

d) Czy \(X\) i \(Y\) są niezależne?

Rozwiązanie

a) \(P(X=0,Y \le 1) = \frac{1}{6} + \frac{1}{4} = \frac{5}{12}.\)

b) Dopisałem do tabeli w treści zadania.

c) \(P(Y=1|X=0) = \frac{P(Y=1,X=0)}{P(X = 0)} = \frac{\frac{1}{4}}{\frac{13}{24}} = \frac{6}{13}.\)

d) Zmienne nie są niezależne bo \(p_{.0}p_{0.} \ne p_{00}.\)

Zadanie 4

Rozważmy dwie zmienne losowe \(X\) oraz \(Y\) z funkcją prawdopodobieństwa podaną w tabeli.

	\(Y=2\)	\(Y=4\)	\(Y=5\)	\(p_{.k}\)
\(X=1\)	\(\frac{1}{12}\)	\(\frac{1}{24}\)	\(\frac{1}{24}\)	\(\frac{1}{6}\)
\(X=2\)	\(\frac{1}{6}\)	\(\frac{1}{12}\)	\(\frac{1}{8}\)	\(\frac{3}{8}\)
\(X=3\)	\(\frac{1}{4}\)	\(\frac{1}{8}\)	\(\frac{1}{12}\)	\(\frac{11}{24}\)
\(p_{i.}\)	\(\frac{1}{2}\)	\(\frac{1}{4}\)	\(\frac{1}{4}\)	1

a) Znajdź \(P(X \le 2, Y \le 4)\).

b) Znajdź rozkłady brzegowe zmiennych \(X\) oraz \(Y\).

c) Znajdź \(P(Y=2|X=1)\).

d) Czy \(X\) i \(Y\) są niezależne?

Rozwiązanie

a) \(P(X \le 2, Y \le 4) = P_{XY}(1,2)+P_{XY}(1,4)+P_{XY}(2,2)+P_{XY}(2,4)=\frac{1}{12} + \frac{1}{24} + \frac{1}{6} + \frac{1}{12} = \frac{3}{8}.\)

b) Dopisałem w tabeli powyżej.

c) \(P(Y=2|X=1) = \frac{P_{XY}(X=1, Y=2)}{P_X(X=1)} = \frac{\frac{1}{12}}{\frac{1}{6}} = \frac{1}{2}.\)

d) Zmienne nie są niezależne bo:

\(P_{XY}(X=2,Y=2)=\frac{1}{6} \ne P_X(X=2)P_Y(Y=2)=\frac{3}{16}.\)

Zadanie 5

Niech dwuwymiarowa zmienna losowa \((X, Y)\) ma rozkład podany w tabelce:

\(y_k\) \ \(x_i\)	2	3	3.5	4	5
2	\(\frac{3}{35}\)	\(\frac{2}{35}\)	\(\frac{1}{35}\)	0	0
3	\(\frac{1}{35}\)	\(\frac{10}{35}\)	\(\frac{2}{35}\)	\(\frac{1}{35}\)	0
3.5	0	\(\frac{1}{35}\)	\(\frac{5}{35}\)	\(\frac{1}{35}\)	\(\frac{1}{35}\)
4	0	0	0	\(\frac{3}{35}\)	\(\frac{2}{35}\)
5	0	0	0	\(\frac{1}{35}\)	\(\frac{1}{35}\)

gdzie \(X\) jest oceną klasówki z matematyki losowo wybranego ucznia pewnej klasy, \(Y\) zaś oceną klasówki z fizyki. Wyznaczyć rozkład warunkowy zmiennej losowej \(Y\) pod warunkiem, że \(X=4\).

Rozwiązanie

Mamy:

\(p_{4.}=P(X=4)=\frac{6}{35}.\)

Teraz:

\(P(Y=y_k|X=4) = \frac{P(Y=y_k, X=4)}{P(X=4)} = \frac{P(Y=y_k, X=4)}{\frac{6}{35}},\)

\(P(Y=2|X=4) = 0,\)

\(P(Y=3|X=4) = \frac{1}{6},\)

\(P(Y=3.5|X=4) = \frac{1}{6},\)

\(P(Y=4|X=4) = \frac{3}{6},\)

\(P(Y=5|X=4) = \frac{1}{6}.\)

Zadanie 6

Z talii 52 kart wylosowano 1 kartę. Niech zmienna losowa \(X\) przyjmuje wartości równe liczbie wylosowanych asów, zaś \(Y\) - liczbę wylosowanych pików. Wyznaczyć rozkład prawdopodobieństwa dwuwymiarowej zmiennej losowej \((X, Y)\) i rozkłady brzegowe. Czy zmienne są niezależne?

Rozwiązanie

Ponieważ losujemy tylko 1 kartę, każda ze zmiennych \(X\), \(Y\) może przyjmować z dodatnim prawdopodobieństwem tylko dwie wartości 0 albo 1.

Oznaczmy możliwe zdarzenia:

\(A\) - wylosowanie asa pik,

\(B\) - wylosowanie pika, który nie jest asem,

\(C\) - wylosowanie asa, który nie jest pikiem,

\(D\) - wylosowanie karty, która nie jest asem i nie jest pikiem.

\(P(A) = P(X=1,Y=1) = \frac{1}{52},\)

\(P(B) = P(X=0,Y=1) = \frac{12}{52},\)

\(P(C) = P(X=1,Y=0) = \frac{3}{52},\)

\(P(D) = P(X=0,Y=0) = \frac{36}{52}.\)

\(y_k\) \ \(x_n\)	0	1	\(p_{.k}\)
0	\(\frac{36}{52}\)	\(\frac{3}{52}\)	\(\frac{39}{52}\)
1	\(\frac{12}{52}\)	\(\frac{1}{52}\)	\(\frac{13}{52}\)
\(p_{\text{i.}}\)	\(\frac{48}{52}\)	\(\frac{4}{52}\)	1

Zmienne są niezależne, ponieważ dla każdej ustalonej wartości \(X\) i \(Y\):

\(P(X,Y) = P(X)P(Y)\), np.:

\(P(X=0,Y=0) = \frac{36}{52} = \frac{48}{52} \cdot \frac{39}{52} = P(X=0)P(Y=0)\)

Zadanie 7

Pewien mechanizm składa się z dwóch kół zębatych: dużego i małego. Warunki techniczne przy montażu urządzenia zostają naruszone, jeśli w obu kołach występują dodatnie odchylenia grubości zębów od nominalnego wymiaru. Robotnik dysponuje 2 kołami zębatymi dużymi: “plusowym” i “minusowym” i dwoma małymi “plusowym” i “minusowym”. Rozważmy zero-jedynkowe zmienne losowe \(X\) i \(Y\): zmienna losowa \(X\) przyjmuje wartość 1, jeśli robotnik wylosuje duże koło “plusowe” i 0 jeśli duże koło “minusowe”. Analogicznie określona jest zmienna losowa \(Y\) w przypadku koła małego.

a) Wyznaczyć dystrybuantę \(F\) dwuwymiarowej zmiennej losowej \((X, Y)\).

b) Obliczyć prawdopodobieństwo naruszenia warunków technicznych przy montażu mechanizmu.

Rozwiązanie

a)

Na początku wyznaczę rozkład zmiennej losowej \((X, Y)\). Zmienna \((X, Y)\) przyjmuje wartości \((0, 0), (1, 0), (0, 1), (1, 1)\) z prawdopodobieństwami:

\(P(X = 0, Y = 0) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4},\)

\(P(X = 1, Y = 0) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4},\)

\(P(X = 0, Y = 1) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4},\)

\(P(X = 1, Y = 1) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4}.\)

W tabeli wygląda to następująco:

\(y_k\) \ \(x_i\)	0	1
0	\(\frac{1}{4}\)	\(\frac{1}{4}\)
1	\(\frac{1}{4}\)	\(\frac{1}{4}\)

Korzystając z wzoru nr (1) wyznaczam dystrybuantę:

\(y\) \ \(x\)	\((-\infty, 0]\)	\((0,1]\)	\((1, \infty)\)
\((-\infty,0]\)	0	0	0
\((0, 1]\)	0	\(\frac{1}{4}\)	\(\frac{1}{2}\)
\((1,\infty)\)	0	\(\frac{1}{2}\)	1

b)

Naruszenie warunków technicznych montażu nastąpi wtedy, gdy robotnik wybierze losowo duże koło zębate plusowe i małe koło plusowe:

\(P(X = 1, Y = 1) = \frac{1}{2}\cdot\frac{1}{2} = \frac{1}{4}\).

Zadanie 8

Rzucamy jedną kostką do gry. Niech zmienna losowa \(X\) przyjmuje wartość 0, gdy wyrzucimy parzystą liczbę oczek (zdarzenie \(A\)), oraz wartość 1, gdy wyrzucimy nieparzystą liczbę oczek (\(A'\)), zmienna losowa \(Y\) przyjmuje wartość 1, gdy liczba rzuconych oczek jest podzielna przez 3 (\(B\)), oraz wartość 2, gdy liczba oczek nie jest podzielna przez 3 (\(B'\)). Zbadać niezależność zmiennych losowych \(X\) i \(Y\).

Rozwiązanie

Dwuwymiarowa zmienna losowa \((X, Y)\) przyjmuje wartości: \((0,1)\), \((0,2)\), \((1,1)\), \((1,2)\) z prawdopodobieństwami:

\(P(X=0, Y=1) = P(A \cap B) = \frac{1}{6},\)

\(P(X=0, Y=2) = P(A \cap B') = \frac{2}{6} = \frac{1}{3},\)

\(P(X=1, Y=1) = P(A' \cap B) = \frac{1}{6},\)

\(P(X=1, Y=2) = P(A' \cap B') = \frac{2}{6} = \frac{1}{3}.\)

Przedstawiam otrzymane wyniki w tabelce dwudzielczej i wyznaczam rozkłady brzegowe poszczególnych zmiennych

\(y_k\) \ \(x_i\)	0	1	\(p_{.k}\)
1	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{3}\)
2	\(\frac{1}{3}\)	\(\frac{1}{3}\)	\(\frac{2}{3}\)
\(p_{i.}\)	\(\frac{1}{2}\)	\(\frac{1}{2}\)	1

Zauważmy, że dla \(\underset{i = 1, 2 \ k = 1, 2}{\forall} \ p_{ik} = p_{i.}p_{.k}\), a więc \(X\), \(Y\) są niezależnymi zmiennymi losowymi.

Zadanie 9

Niech zmienne losowe \(X\) i \(Y\) mają rozkłady zero-jedynkowe o parametrach odpowiednio \(p\) i \(q\), gdzie \(0 < p, q < 1\) oraz będą niezależne. Znajdź łączną gęstość prawdopodobieństwa oraz łączną dystrybuantę zmiennych losowych \(X\) i \(Y\).

Rozwiązanie

Zmienne losowe \(X\) i \(Y\) przyjmują wartości 0 oraz 1. Wszystkie możliwe kombinacje to:

\(R_{XY}=\{(0,0),(0,1),(1,0),(1,1)\}.\)

Ponieważ zmienne losowe \(X\) i \(Y\) są niezależne to:

\(p_{ik} = p_{i.}p_{.k} \ \text{ dla } \ i,k=0,1.\)

Ostatecznie:

\(P(0,0)=P_X(0)P_Y(0)=(1−p)(1−q),\)

\(P(0,1)=P_X(0)P_Y(1)=(1−p)q,\)

\(P(1,0)=P_X(1)P_Y(0)=p(1−q),\)

\(P(1,1)=P_X(1)P_Y(1)=pq.\)

Teraz obliczę dystrybuantę:

\(F_{XY}(x,y)=P(X≤x,Y≤y).\)

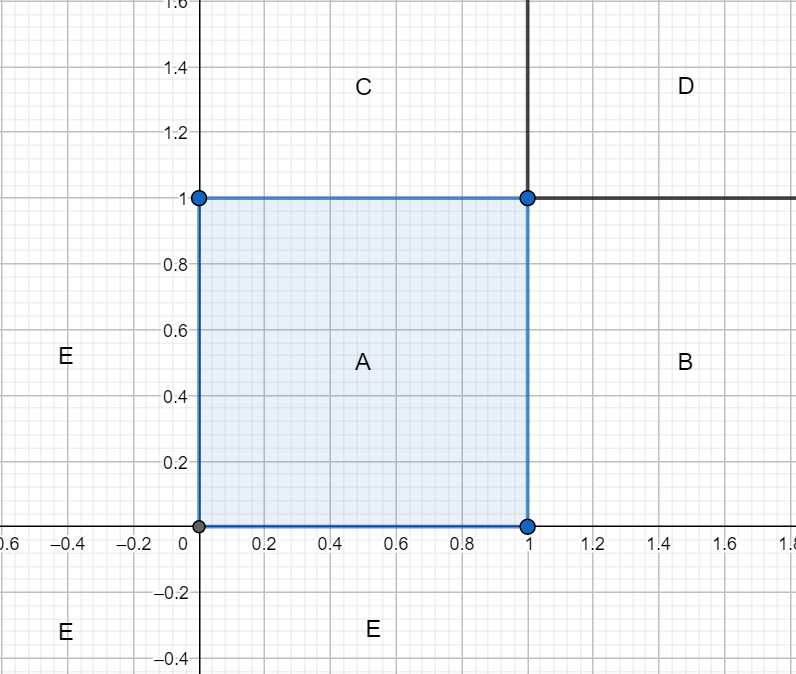
1. \((x, y) \in A\)

   \(F_{XY}(x,y)=P(X \le x,Y \le y)=P(X=0,Y=0)=P(X=0)P(Y=0)=(1−p)(1−q).\)

2. \((x, y) \in B\)

   \(F_{XY}(x,y)=P(X \le x,Y \le y)=P(X \le 1,Y=0)=P(Y=0)=1−q.\)

3. \((x, y) \in C\)

   \(F_{XY}(x,y)=P(X \le x,Y \le y)=P(X=0,Y \le 1)=P(X=0)=1−p.\)

4. \((x, y) \in D\)

   \(F_{XY}(x,y)=P(X \le x,Y \le y)=P(X \le 1,Y \le 1)=1.\)

5. \((x, y) \in E\)

   \(F_{XY}(x, y) = 0\)

Ostatecznie:

\(F_{XY}(x, y) = \begin{cases} 0 & E=\{(x,y): x < 0 \vee y < 0\}, \\ (1−p)(1−q) & A=\{(x,y): 0 \le x < 1 \wedge 0 \le y < 1\}, \\ 1−q & B=\{(x,y): x \ge 1 \wedge 0 \le y < 1\}, \\ 1−p & C=\{(x,y): 0 \le x < 1 \wedge y \ge 1\}, \\ 1 & D=\{(x,y): x \ge 1 \wedge y \ge 1\}, \\ \end{cases}\)

## Zadanie 10

Dwuwymiarowa zmienna losowa $(X,Y)$ charakteryzuje losowo wybranego w pewnym miesiącu klienta banku. Zmienna losowa $X$ oznacza liczbę rodzajów funduszy inwestycyjnych, które posiada klient, natomiast zmienna losowa $Y$ przyjmuje wartość $y=1$, jeśli klient posiada jakąkolwiek lokatę, a $y=0$, gdy klient nie posiada lokaty. Funkcję prawdopodobieństwa łącznego zmiennej $(X,Y)$ określa tabela:

|$y_k$ \ $x_i$  |0   |1   |2   |3   |$p_{.k}$|
|---|---|---|---|---|---|
|0       |0.02|0.07|0.06|0.01|0.16|
|1       |0.01|0.5 |0.3 |0.03|0.84|
|$p_{i.}$|0.03|0.57|0.36|0.04|1   |

a) Oblicz prawdopodobieństwo warunkowe, że losowo wybrany klient posiada jakikolwiek fundusz inwestycyjny, jeśli wiadomo, że nie ma on lokaty.

b) Oblicz wariancję $Var(X)$.

c) Czy zmienne losowe $X$, $Y$ są niezależne.

d) Znajdź $F(1, 1.5)$.

```{dropdown} Rozwiązanie

a)

$P(X \ge 1 | Y=0) = \frac{P(X \ge 1, Y=0)}{P(Y=0)} = \frac{P(1, 0)+P(2, 0) + P(3, 0)}{P(Y=0)} = \frac{0.07+0.06+0.01}{0.16} = \frac{0.14}{0.16} = 0.875$

b)

$E(X) = 0\cdot0.03 + 1\cdot0.57 + 2\cdot0.36 + 3\cdot0.04 = 1.41,$

$E(X^2) = 0^2\cdot0.03 + 1^2\cdot0.57 + 2^2\cdot0.36 + 3^2\cdot0.04 = 2.37,$

$Var(X) = 2.37 - 1.41^2 = 0.3819.$

c)

$0.02 \ne 0.01\cdot0.16$

Więc zmienne losowe nie są niezależne.

d)

$F(1, 1.5) = P(X \le 1, Y \le 1.5) = 0.02 + 0.07 + 0.01 + 0.5 = 0.6$.

Zadanie 11

Rzucamy kością do gry. Niech \(X\) będzie liczbą wyrzuconych oczek. Znajdź gęstość \(X\) pod warunkiem, że wyrzucona liczba oczek będzie mniejsza niż 5.

Rozwiązanie

Korzystam z:

\(P_{X|A}(X=x_i|A) = P_{X|A}(X=x_i|X<5)=\frac{P_X(X=x_i, X < 5)}{P(X < 5)},\)

\(P(A) = P(X < 5) = \frac{4}{6}\)

\(P_{X|A}(X=1|X < 5)=\frac{P_X(X=1, X < 5)}{P(X < 5)} = \frac{\frac{1}{6}}{\frac{4}{6}} = \frac{1}{4},\)

\(P_{X|A}(X=1|X < 5) = P_{X|A}(X=2|X < 5) = P_{X|A}(X=3|X < 5) = P_{X|A}(X=4|X < 5) = \frac{1}{4}\)

\(P_{X|A}(X=5|X < 5)=\frac{P_X(X=5, X < 5)}{P(X < 5)} = \frac{0}{\frac{4}{6}} = 0,\)

\(P_{X|A}(X=5|X < 5) = P_{X|A}(X=6|X < 5) = 0.\)

Zadanie 12

Rozważmy zbiór punktów \(G\) zdefiniowany następująco:

\(G=\{(x,y):x,y \in Z,|x|+|y| \le 2\}.\)

Zakładamy, że wybieramy punkt \((X, Y)\) całkowicie losowo. Stąd prawdopodobieństwo wybrania dowolnego punktu wynosi \(\frac{1}{13}\).

a) Znajdź rozkład łączny oraz rozkłady brzegowe zmiennych \(X\) i \(Y\).

b) Znajdź gęstość \(X\) pod warunkiem \(Y = 1\).

c) Czy zmienne \(X\) i \(Y\) są niezależne?

Rozwiązanie

a)

Przedstawię wyniki w tabeli:

\(x_i\) \ \(y_k\)	-2	-1	0	1	2	\(p_{.k}\)
-2	0	0	\(\frac{1}{13}\)	0	0	\(\frac{1}{13}\)
-1	0	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	0	\(\frac{3}{13}\)
0	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{5}{13}\)
1	0	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	0	\(\frac{3}{13}\)
2	0	0	\(\frac{1}{13}\)	0	0	\(\frac{1}{13}\)
\(p_{i.}\)	\(\frac{1}{13}\)	\(\frac{3}{13}\)	\(\frac{5}{13}\)	\(\frac{3}{13}\)	\(\frac{1}{13}\)	1

Można też zapisać wzorami:

\(P_{XY}(x, y) = \begin{cases} \frac{1}{13} & (x, y) \in G, \\ 0 & \text{poza tym}. \\ \end{cases}\)

\(P_X(k)=P_Y(k)=\frac{5−2|k|}{13}, \ \text{dla } k=−2,−1,0,1,2.\)

b)

\(P_{X|Y}(X=x_i|Y=y_k) = \frac{p_{ik}}{p_{.k}},\)

\(P_{X|Y}(X=-1|Y=1) = \frac{\frac{1}{13}}{\frac{3}{13}} = \frac{1}{3},\)

\(P_{X|Y}(X=0|Y=1) = \frac{1}{3},\)

\(P_{X|Y}(X=1|Y=1) = \frac{1}{3}.\)

c)

Zmienne \(X\) i \(Y\) nie są niezależne bo:

\(\frac{1}{13}\cdot\frac{1}{13} \ne 0.\)

Zadanie 13

Dla danych z poniższej tabeli:

\(x_i\) \ \(y_k\)	-2	-1	0	1	2	\(p_{.k}\)
-2	0	0	\(\frac{1}{13}\)	0	0	\(\frac{1}{13}\)
-1	0	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	0	\(\frac{3}{13}\)
0	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{5}{13}\)
1	0	\(\frac{1}{13}\)	\(\frac{1}{13}\)	\(\frac{1}{13}\)	0	\(\frac{3}{13}\)
2	0	0	\(\frac{1}{13}\)	0	0	\(\frac{1}{13}\)
\(p_{i.}\)	\(\frac{1}{13}\)	\(\frac{3}{13}\)	\(\frac{5}{13}\)	\(\frac{3}{13}\)	\(\frac{1}{13}\)	1

Znajdź:

a) \(E[X|Y=1]\),

b) \(E[X|−1 < Y < 2]\),

c) \(E[|X||−1 < Y < 2]\).

Rozwiązanie

a) \(E[X|Y=1] = \sum\limits_i x_i P_{X|Y}(X=x_i|Y=1) = -2\cdot0 -1\cdot\frac{1}{3}+0\cdot\frac{1}{3}+1\cdot\frac{1}{3}+2\cdot0 = 0\)

b) \(E[X|−1 < Y < 2] = \sum\limits_i x_i P_{X|Y}(X=x_i|−1 < Y < 2),\)

\(P_{X|Y}(X=x_i|−1 < Y < 2) = \frac{P_{XY}(X=x_i|−1 < Y < 2)}{P_Y(−1 < Y < 2)},\)

\(P_Y(−1 < Y < 2) = \frac{8}{13},\)

\(P_{X|Y}(X=-2|−1 < Y < 2) = \frac{\frac{1}{13}}{\frac{8}{13}} = \frac{1}{8},\)

\(P_{X|Y}(X=-1|−1 < Y < 2) = \frac{\frac{2}{13}}{\frac{8}{13}} = \frac{2}{8},\)

\(P_{X|Y}(X=0|−1 < Y < 2) = \frac{\frac{2}{13}}{\frac{8}{13}} = \frac{2}{8},\)

\(P_{X|Y}(X=1|−1 < Y < 2) = \frac{\frac{2}{13}}{\frac{8}{13}} = \frac{2}{8},\)

\(P_{X|Y}(X=2|−1 < Y < 2) = \frac{\frac{1}{13}}{\frac{8}{13}} = \frac{1}{8},\)

\(E[X|−1 < Y < 2] = -2\cdot\frac{1}{8} -1\cdot\frac{2}{8}+0\cdot\frac{2}{8}+1\cdot\frac{2}{8}+2\cdot\frac{1}{8} = 0\)

c)

\(E[|X| \ |−1 < Y < 2] = \sum\limits_i |x_i| P_{X|Y}(X=x_i|−1 < Y < 2)\)

\(= 2\cdot\frac{1}{8} + 1\cdot\frac{2}{8} + 0\cdot\frac{2}{8} + 1\cdot\frac{2}{8}+ 2\cdot\frac{1}{8} = 1\)

Zadanie 14

W worku znajduje się 40 niebieskich kul oraz 60 czerwonych kul. Losujemy 10 kul bez zwracania. Niech \(X\) to liczba wylosowanych kul niebieskich a \(Y\) to liczba wylosowanych kul niebieskich. Znaleźć łączną funkcję prawdopodobieństwa zmiennych \(X\) i \(Y\).

Rozwiązanie

Jest to rozkład hipergeometryczny:

\(P_{XY}(i, j)=\begin{cases} \frac{ {40\choose i}{60\choose j }}{ {100\choose10} } & i+j=10; \ i,j\in\mathbb{Z}; \ i,j \ge 0, \\ 0 & \text{p.p.} \\ \end{cases}\)

Zadanie 15

Niech \(X\) i \(Y\) będą dyskretnymi zmiennymi losowymi o wartościach ze zbioru:

\(R_{XY}=\{(i,j)∈\mathbb{Z}^2;i,j≥0;|i−j|≤1\},\)

o łącznej funkcji prawdopodobieństwa:

\(P_{XY}(i,j)=\frac{1}{6⋅2^{\min(i,j)} }, \ \text{dla } (i,j)\in R_{XY}.\)

a) Znajdź rozkłady brzegowe \(P_X(i)\) oraz \(P_Y(j)\).

b) Znajdź \(P(X=Y|X<2)\).

c) Znajdź \(P(1 \le X^2+Y^2 \le 5)\).

d) Znajdź \(P(X=Y)\).

e) Znajdź \(E[X|Y=2]\).

f) Znajdź \(Var(X|Y=2)\).

Rozwiązanie

a)

Przez symetrię widać, że \(X\) i \(Y\) mają takie same funkcje prawdopodobieństwa. Możemy zapisać:

\(P_X(0)=P_{XY}(0,0)+P_{XY}(0,1)=\frac{1}{6}+\frac{1}{6}=\frac{1}{3},\)

\(P_X(1)=P_{XY}(1,0)+P_{XY}(1,1)+P_{XY}(1,2)=\frac{1}{6}(1+\frac{1}{2}+\frac{1}{2})=\frac{1}{3},\)

\(P_X(2)=P_{XY}(2,1)+P_{XY}(2,2)+P_{XY}(2,3)=\frac{1}{6}(\frac{1}{2}+\frac{1}{4}+\frac{1}{4})=\frac{1}{6},\)

\(P_X(3)=P_{XY}(3,2)+P_{XY}(3,3)+P_{XY}(3,4)=\frac{1}{6}(\frac{1}{4}+\frac{1}{8}+\frac{1}{8})=\frac{1}{12}.\)

W ogólności:

\(P_X(k) = P_Y(k) = \begin{cases} \frac{1}{3}, & k=0 \\ \frac{1}{3\cdot2^{k-1} }, & k=1,2,3,... \\ 0, & \text{p.p.} \\ \end{cases}\)

b)

\(P(X=Y|X < 2)=\frac{P(X=Y,X < 2)}{P(X < 2)}\)

\(=\frac{P_{XY}(0,0)+P_{XY}(1,1)}{P_X(0)+P_X(1)}=\frac{\frac{1}{6}+\frac{1}{12} }{\frac{1}{3}+\frac{1}{3} }=\frac{3}{8}\).

c)

\(P(1 \le X^2+Y^2 \le 5)\)

\(=P_{XY}(0,1)+P_{XY}(1,0)+P_{XY}(1,1)+P_{XY}(1,2)+P_{XY}(2,1)\)

\(=\frac{1}{6}+\frac{1}{6}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{7}{12}.\)

d)

\(P(X=Y)=\sum\limits_{i=0}^\infty P_{XY}(i,i)=\sum\limits_{i=0}^\infty \frac{1}{6\cdot2^i}=\frac{1}{6}\cdot2=\frac{1}{3}.\)

e)

Aby znaleźć \(E[X|Y=2]\) należy najpierw znaleźć rozkład warunkowy zmiennej \(X\) przy ustalonym \(Y=2\):

\(P_{X|Y}(k|2)=\frac{P_{XY}(k,2)}{P_Y(2)}=6P_{XY}(k,2),\)

mamy:

\(P_{X|Y}(k|2) = \begin{cases} \frac{1}{2}, & k=1 \\ \frac{1}{4}, & k=2,3 \\ 0, & \text{p.p.} \\ \end{cases}\)

stąd:

\(E[X|Y=2]=1⋅\frac{1}{2}+2⋅\frac{1}{4}+3⋅\frac{1}{4}=\frac{7}{4}.\)

f)

\(E[X^2|Y=2]=1⋅\frac{1}{2}+4\frac{1}{4}+9⋅\frac{1}{4}=\frac{15}{4},\)

stąd:

\(Var(X)=E[X^2|Y=2]−(E[X|Y=2])^2=\frac{15}{4}−\frac{49}{16}=\frac{11}{16}.\)

Zadanie 16

Niech \(X \sim Geo(p)\). Znajdź \(EX\) poprzez warunkowanie wyniku pierwszego rzutu monetą.

Rozwiązanie

\(O\) - wyrzucenie orła,

\(R\) - wyrzucenie reszki.

\(P(O) = p.\)

Rzucamy monetą aż do momentu wyrzucenia orła. \(X\) jest całkowitą liczbą rzutów.

Stosuję:

\(EX=\sum\limits_i E[X|B_i]P(B_i).\)

\(EX=E[X|O]P(O)+E[X|R]P(R)=pE[X|O]+(1−p)E[X|R]=p⋅1+(1−p)(EX+1).\)

W powyższym, \(E[X|T]=EX + 1\), ponieważ rzuty są niezależne to jeżeli w pierwszym rzucie wypadnie reszka to w drugim rzucie zaczynamy eksperyment tak jakby od początku. Rozwiązując ze względu na \(EX\) otrzymujemy:

\(EX=\frac{1}{p}.\)

Zadanie 17

Rzucamy monetą z prawdopodobieństwem wyrzucenia reszki \(P(R) = p\). Rzucamy nieprzerwanie aż wyrzucimy dwie reszki pod rząd. Niech \(X\) będzie zmienną losową opisującą całkowitą liczbę rzutów. Znajdź \(EX\).

Rozwiązanie

Podobnie jak w poprzednim zadaniu, warunkowanie pierwszym rzutem:

\(\mu=EX=E[X|R]P(R)+E[X|O]P(O)=E[X|R]p+(1+\mu)(1−p).\)

\(p\mu=pE[X|H]+(1−p)\)

Aby obliczyć \(E[X|R]\) należy teraz warunkować drugim rzutem:

\(E[X | H]=E[X | HH]p + E[X | HT](1 - p) = 2p+(2+\mu)(1−p)=2+(1−p)\mu .\)

Ostatecznie:

\(\mu=EX=1+\frac{p}{p^2}.\)

Zadanie 18

Przypuśćmy, że liczbę klientów wizytujących restaurację w danym dniu opisuje zmienna losowa \(N \sim Poisson(\lambda)\). Załóżmy, że każdy klient kupuje napój z prawdopodobieństwem \(p\) niezależnie od innych klientów i niezależnie od wartości \(N\). Niech \(X\) będzie liczbą klientów, którzy kupili napój. Znajdź \(EX\).

Rozwiązanie

Zgodnie z treścią zadania wnioskujemy, że przy ustalonym \(N=n\) zmienna losowa \(X\) jest sumą \(n\) niezależnych prób Bernoulliego z parametrem \(p\). Stąd przy ustalonym \(N=n\), zmienna losowa \(X\) ma rozkład dwumianowy z parametrami \(n\) i \(p\). Możemy napisać:

\(X|N=n \sim Binomial(n,p).\)

Stąd:

\(P_{X|N}(k|n)={n\choose k}p^k(1−p)^{n−k}.\)

Czyli:

\(E[X|N=n]=np.\)

Stąd z prawa całkowitej wartości oczekiwanej mamy:

\(E[X]=\sum\limits_{n=0}^\infty E[X|N=n]P_N(n)=\sum\limits_{n=0}^\infty npP_N(n)=p \sum\limits_{n=0}^\infty nP_N(n)=pE[N]=p\lambda .\)

Zadanie 19

Dla dwóch zmiennych losowych dyskretnych \(X\) i \(Y\) pokaż, że \(E[X+Y]=EX+EY\).

Rozwiązanie

\(E[X + Y]=\)

\(=\sum\limits_i \sum\limits_k (x_i + y_k) P_{XY}(x_i, y_k)\)

\(=\sum\limits_i \sum\limits_k x_i P_{XY}(x_i, y_k) + \sum\limits_i \sum\limits_k y_k P_{XY}(x_i, y_k)\)

\(=\sum\limits_i x_i \sum\limits_k P_{XY}(x_i, y_k) + \sum\limits_k y_k \sum\limits_i P_{XY}(x_i, y_k)\)

\(=\sum\limits_i x_i P_{X}(x_i) + \sum\limits_k y_k P_{Y}(y_k)\)

\(=EX + EY\)

Powyżej korzystamy z wzoru na rozkład brzegowy.

Zadanie 20

Niech zmienne losowe \(X\) oraz \(Y\) będą niezależne oraz niech pochodzą z rozkładu geometrycznego z parametrem \(p\). Znaleźć funkcję prawdopodobieństwa zmiennej losowej \(Z = X - Y\).

Rozwiązanie

Najpierw wyznaczę punkty skokowe zmiennych \(X\), \(Y\) oraz \(Z\):

\(W_X=W_Y=\mathbb{N}=\{1,2,3,\dots \},\)

stąd:

\(W_Z=\mathbb{Z}=\{\dots,−3,−2,−1,0,1,2,3,\dots \}.\)

Ponieważ \(X,Y \sim Geometric(p),\) mamy:

\(P_X(k)=P_Y(k)=pq^{k−1}, \ \text{ dla } k=1,2,3,\dots ,\)

gdzie \(q=1−p\). Dla każdego \(k \in Z\) możemy napisać:

\(P_Z(k)=P(Z=k)=P(X−Y=k)=P(X=Y+k)= \)

\(= \sum\limits_{j=1}^\infty P(X=Y+k|Y=j)P(Y=j)\)

\(= \sum\limits_{j=1}^\infty P(X=j+k|Y=j)P(Y=j)\)

\(= \sum\limits_{j=1}^\infty P(X=j+k)P(Y=j)\)

\(= \sum\limits_{j=1}^\infty P_X(j+k)P_Y(j).\)

W powyższym korzystamy z prawdopodobieństwa całkowitego oraz niezależności zmiennych losowych.

Dla \(k > 0\):

\(P_Z(k) = \sum\limits_{j=1}^\infty P_X(j+k)P_Y(j)\)

\(= \sum\limits_{j=1}^\infty pq^{j+k−1}pq^{j−1} = p^2q^k \sum\limits_{j=1}^\infty q^{2(j−1)}\)

\(= p^2q^k \frac{1}{1−q^2} = \frac{p(1−p)^k}{2−p}.\)

Dla \(k < 0\):

\(P_X(j+k)=0 \ \ \text{dla } j < -k+1\)

\(P_Z(k) = \sum\limits_{j=1}^\infty P_X(j+k)P_Y(j)\)

\(= \sum\limits_{j=-k+1}^\infty pq^{j+k−1}pq^{j−1} = p^2\sum\limits_{j=-k+1}^\infty q^{k+2(j−1)}\)

\(= p^2[q^{−k}+q^{−k+2}+q^{−k+4}+\dots] = p^2q^{−k}[1+q^2+q^4+\dots]\)

\(= \frac{p(1−p)^{-k} }{(2−p)}.\)

Ostatecznie:

\(P_Z(k) = \begin{cases} \frac{p(1−p)^{|k|} }{(2−p)} & \text{ dla } k \in \mathbb{Z}, \\ 0 & \text{poza tym}. \\ \end{cases}\)

Zadanie 21

Niech zmienne losowe \(X\) oraz \(Y\) będą niezależne oraz niech pochodzą z rozkładu geometrycznego z parametrem \(p\). Niech \(Z = \frac{X}{Y}\).

a) Znajdź punkty skokowe zmiennej \(Z\).

b) Znajdź funkcję prawdopodobieństwa zmiennej \(Z\).

c) Oblicz \(EZ\).

Rozwiązanie

a)

\(R_Z=\{\frac{m}{n}:m,n \in \mathbb{N}\}\)

b)

\(P_Z(\frac{m}{n})=\sum\limits_{k=1}^\infty P(X=mk,Y=nk)\)

\(=\sum\limits_{k=1}^\infty P(X=mk)P(Y=nk)=\sum\limits_{k=1}^\infty pq^{mk−1}pq^{nk−1}\)

\(=p^2q^{−2}\sum\limits_{k=1}^\infty q^{(m+n)k}=\frac{p^2 q^{m+n−2} }{1−q^{m+n} }\)

\(=\frac{p^2(1−p)^{m+n−2} }{1−(1−p)^{m+n} }.\)

c)

Dwa wzory użyte w obliczeniach:

\(\sum\limits_{k=1}^\infty kx^{k−1}= \frac{1}{(1−x)^2}, \ \text{dla } |x| < 1,\)

\(\sum\limits_{k=1}^\infty \frac{x^k}{k} = −\ln(1−x), \ \text{dla } |x| < 1.\)

\(E[XY]= \sum\limits_{n=1}^\infty \sum\limits_{m=1}^\infty mnP(X=m,Y=n)\)

\(= \sum\limits_{n=1}^\infty \sum\limits_{m=1}^\infty \frac{m}{n} p^2 q^{m−1}q^{n−1} = \sum\limits_{n=1} \frac{1}{n} p^2 q^{n−1} \sum\limits_{m=1}^\infty mq^{m−1}\)

\(=\sum\limits_{n=1} \frac{1}{n} p^2 q^{n−1} \frac{1}{(1−q)^2} = \sum\limits_{n=1} \frac{1}{n} q^{n−1}\)

\(= \frac{1}{q} \sum\limits_{n=1} \frac{q^n}{n}= \frac{1}{1−p} ln{\frac{1}{p} }.\)

## Zadanie 22

Rozważmy dwie zmienne losowe $X$ oraz $Y$ z łączną funkcją prawdopodobieństwa podaną w poniższej tabeli:

|$x_i$ \ $y_k$|0|1|$p_{.k}$|
|---|---|---|---|
|0       |$\frac{1}{5}$|$\frac{2}{5}$|$\frac{3}{5}$|
|1       |$\frac{2}{5}$|0            |$\frac{2}{5}$|
|$p_{i.}$|$\frac{3}{5}$|$\frac{2}{5}$|1            |

Niech $Z=E[X|Y]$.

a) Znajdź brzegowe funkcje prawdopodobieństwa zmiennych $X$ i $Y$.

b) Znajdź $P_{X|Y}(x|0)$ i $P_{X|Y}(x|1)$.

c) Znajdź funkcję prawdopodobieństwa zmiennej $Z$.

d) Znajdź $E[Z]$ oraz sprawdź, że $E[Z]=E[X]$. 

e) Znajdź $Var(Z)$.

```{dropdown} Rozwiązanie

a)

$P_X(X=0)=\frac{1}{5}+\frac{2}{5}=\frac{3}{5}$,

$P_X(X=1)=\frac{2}{5}+0=\frac{2}{5}$,

$P_Y(Y=0)=\frac{1}{5}+\frac{2}{5}=\frac{3}{5}$,

$P_Y(Y=1)=\frac{2}{5}+0=\frac{2}{5}$.

Czyli $X, Y \sim B(1, \frac{2}{5})$, rozkład zero-jedynkowy.

b)

$P_{X|Y}(0|0)=\frac{P_{XY}(X=0,Y=0)}{P_Y(Y=0)}=\frac{\frac{1}{5} }{\frac{3}{5} }=\frac{1}{3}$,

$P_{X|Y}(1|0)=\frac{P_{XY}(X=1,Y=0)}{P_Y(Y=0)}=\frac{\frac{2}{5} }{\frac{3}{5} }=\frac{2}{3}$,

Czyli $X|Y=0 \sim B(1, \frac{2}{3})$.

$P_{X|Y}(0|1)=\frac{P_{XY}(X=0,Y=1)}{P_Y(Y=1)}=\frac{\frac{2}{5} }{\frac{2}{5} }=1$,

$P_{X|Y}(1|1)=\frac{P_{XY}(X=1,Y=1)}{P_Y(Y=1)}=\frac{0}{\frac{2}{5} }=0$.

Czyli $X|Y=1 \sim B(1, 0)$.

c)

$Z=E[X|Y]=\begin{cases}
E[X|Y=0] & \text{jeżeli } Y=0, \\
E[X|Y=1] & \text{jeżeli } Y=1. \\
\end{cases}$

$E[X|Y=0] = \sum\limits_i x_i P_{X|Y}(x_i|0) = 0 \cdot \frac{1}{3} + 1 \cdot \frac{2}{3} = \frac{2}{3}$,

$E[X|Y=1] = \sum\limits_i x_i P_{X|Y}(x_i|1) = 0 \cdot 1 + 1 \cdot 0 = 0$.

$P(Y=0)=\frac{3}{5}$,

$P(Y=1)=\frac{2}{5}$.

Stąd:

$Z=E[X|Y]=\begin{cases}
\frac{2}{3} & \text{z prawdopodobieństwem } \frac{3}{5}, \\
0           & \text{z prawdopodobieństwem } \frac{2}{5}, \\
\end{cases}$

ostatecznie:

$P_Z(z)=\begin{cases}
\frac{3}{5} & \text{dla } z = \frac{2}{3}, \\
\frac{2}{5} & \text{dla } z = 0, \\
0           & \text{dla pozostałych}. \\
\end{cases}$

d)

$E[Z]=\frac{2}{3}\cdot\frac{3}{5}+0\cdot\frac{2}{5} = \frac{2}{5}$,

$E[X]=0 \cdot \frac{3}{5} + 1\cdot\frac{2}{5} = \frac{2}{5}$,

$E[X] = E[Z] = E[E[X|Y]]$.

e)

$E[Z^2]=\frac{4}{9}⋅\frac{3}{5}+0⋅\frac{2}{5}=\frac{4}{15}$,

$Var(Z) = \frac{4}{15} - \frac{4}{25} = \frac{8}{75}$.

Zadanie 23

Niech \(X\) i \(Y\) będą dwoma zmiennymi losowymi a \(g\) i \(h\) będą dwoma funkcjami. Pokaż, że \(E[g(X)h(Y)|X]=g(X)E[h(Y)|X]\).

Rozwiązanie

Przy ustalonym \(X=x\) mamy:

\(E[g(X)h(Y)|X]=E[g(X)h(Y)|X=x]=E[g(x)h(Y)|X=x]=g(x)E[h(Y)|X=x]\)

W ogólności dla zmiennej losowej \(X\) możemy zapisać:

\(E[g(X)h(Y)|X]=g(X)E[h(Y)|X]\).

Zadanie 24

Niech zmienne losowe \(X\), \(Y\) oraz \(Z=E[X|Y]\) będą takie jak w zadaniu nr 10. Niech ponadto \(V=Var(X|Y)\).

a) Znajdź funkcję prawdopodobieństwa zmiennej \(V\).

b) Znajdź \(EV\).

c) Sprawdź, że \(Var(X)=E(V)+Var(Z)\).

Rozwiązanie

Mamy:

\(X,Y ∼ B(1, \frac{2}{5})\),

\(X|Y=0∼B(1, \frac{2}{3})\),

\(X|Y=1∼B(1, 0)\),

\(Var(Z)=\frac{8}{75}\).

a)

\(V=Var[X|Y]=\begin{cases} Var[X|Y=0] & \text{jeżeli } Y=0, \\ Var[X|Y=1] & \text{jeżeli } Y=1. \\ \end{cases}\)

\(V=Var[X|Y]=\begin{cases} Var[X|Y=0] & \text{z prawdopodobieństwem } \frac{3}{5}, \\ Var[X|Y=1] & \text{z prawdopodobieństwem } \frac{2}{5}. \\ \end{cases}\)

Ponieważ \(X|Y=0∼B(1, \frac{2}{3})\):

\(Var[X|Y=0] = \frac{2}{3}\cdot\frac{1}{3} = \frac{2}{9}\).

Ponieważ \(X|Y=1∼B(1, 0)\):

\(Var[X|Y=1] = 0\cdot1 = 0\).

Stąd:

\(V=Var[X|Y]=\begin{cases} \frac{2}{9} & \text{z prawdopodobieństwem } \frac{3}{5}, \\ 0 & \text{z prawdopodobieństwem } \frac{2}{5}, \\ \end{cases}\)

ostatecznie:

\(P_V(v)=\begin{cases} \frac{3}{5} & \text{dla } v = \frac{2}{9}, \\ \frac{2}{5} & \text{dla } v = 0, \\ 0 & \text{dla pozostałych}. \\ \end{cases}\)

b)

\(E[V]=\frac{2}{9}⋅\frac{3}{5}+0⋅\frac{2}{5}=\frac{2}{15}\)

c)

\(Var(X) = \frac{2}{5}\cdot \frac{3}{5} = \frac{6}{25},\)

\(EV = \frac{2}{5},\)

\(Var(Z) = \frac{8}{75},\)

stąd:

\(Var(X)=E(V)+Var(Z).\)

Zadanie 25

Niech \(N\) będzie liczbą klientów wizytujących pewien sklep w danym dniu. Załóżmy, że znamy \(EN\) oraz \(Var(N)\). Niech \(X_i\) będzie sumą pieniędzy jaką średnio wydaje i-ty klient w sklepie. Zakładamy, że \(X_i\) są niezależne między sobą oraz są niezależne od \(N\). Zmienne \(X_i\) mają takie same wartości oczekiwane oraz takie same wariancje:

\(EX_i = EX,\)

\(Var(X_i) = Var(X).\)

Niech:

\(Y = \sum\limits_{i=1}^N X_i,\)

znajdź \(EY\) oraz \(Var(Y).\)

Rozwiązanie

Aby znaleźć \(EY\) nie można bezpośrednio skorzystać z liniowości wartości oczekiwanej ponieważ \(N\) jest zmienną losową. Można natomiast przy ustalonym \(N=n\) użyć liniowości aby znaleźć \(E[Y|N=n]\):

\(EY = E[E[Y|N]]\)

\(= E\left[E\left[\sum\limits_{i=1}^N X_i|N\right]\right] = E\left[\sum\limits_{i=1}^N E[X_i|N]\right]\)

\(= E\left[\sum\limits_{i=1}^N EX_i\right] = E[NEX]\)

\(= ENEX.\)

Do znalezienia wariancji użyjemy prawa całkowitej wariancji:

\(Var(Y) = E[Var(Y|N)] + Var(E[Y|N]) = E[Var(Y|N)] + Var(NEX) = E[Var(Y|N)] + (EX)^2Var(N).\)

Aby znaleźć \(E(Var(Y|N))\) zauważmy, że przy ustalonym \(N=n\), \(Y\) jest sumą \(n\) niezależnych zmiennych losowych. Dla \(n\) niezależnych zmiennych losowych wariancja sumy jest równa sumie wariancji.

\(Var(Y|N) = Var\left(\sum\limits_{i=1}^N X_i|N)\right) = \sum\limits_{i=1}^N Var(X_i|N) = \sum\limits_{i=1}^N Var(X_i) = NVar(X),\)

stąd:

\(E[Var(Y|N)] = E[NVar(X)] = ENVar(X),\)

ostatecznie:

\(Var(Y) = ENVar(X) + (EX)^2Var(N).\)

Zadanie 26

Zmienna losowa \((X, Y)\) ma funkcję prawdopodobieństwa daną tabelą:

\(y_k\) \ \(x_i\)	0	1
-2	0.25	0.25
0	0.25	0.25

Znajdź funkcję prawdopodobieństwa zmiennej losowej:

a) \(Z = X + Y,\)

b) \(Z = 2X^2Y.\)

Rozwiązanie

Punkty skokowe:

\(W_X = \{0, 1\},\)

\(W_Y = \{-2, 0\}.\)

a)

\(W_Z = \{-2, 0, -1, 1\}.\)

\(z_i\)	-2	-1	0	1
\(p_i\)	0.25	0.25	0.25	0.25

b)

\(W_V = \{0, 0, -2, 0\} = \{-2, 0\}.\)

\(z_i\)	-2	0
\(p_i\)	0.25	0.75

Zadanie 27

Niech zmienna losowa \((X,Y)\) oznacza wygrane (w tysiącach zł) w dwu etapach teleturnieju przez losowo wybranego uczestnika konkursu. Funkcję prawdopodobieństwa zmiennej \((X,Y)\) przedstawia tabela:

\(y_k\) \ \(x_i\)	0	5	10	\(p_{.k}\)
0	0.5	0	0	0
1	0.3	0.02	0.01	0.01
3	0.1	0.05	0.02	0.01
\(p_{i.}\)	0.9	0.07	0.03	1

Zmienna losowa \(Z = X + Y\) jest łączną wygraną. Oblicz:

a) wartość oczekiwaną łącznej wygranej,

b) \(Cov(X, Y)\),

c) \(Var(Z)\).

Rozwiązanie

a)

Punkty skokowe:

\(W_X = \{0, 5, 10\},\)

\(W_Y = \{0, 1, 3\}\)

\(W_Z = \{0, 1, 3, 5, 6, 8, 10, 11, 13\}\)

\(E(Z) = E(X + Y) = 0.3 + 3\cdot0.1 + 6\cdot0.2 + 8\cdot0.05 + 11\cdot0.01 + 13\cdot0.02 = 2.57.\)

b)

\(E(XY) = 5\cdot0.02 + 10\cdot0.01 + 15\cdot0.05 + 30\cdot0.02 = 1.55,\)

\(E(X) = 0.33 + 3\cdot0.17 = 0.84,\)

\(E(Y) = 5\cdot0.07 + 10\cdot0.03 = 0.65,\)

\(Cov(X,Y) = 1.55 - 0.84\cdot0.65 = 1.004.\)

c)

\(Var(Z) = Var(X+Y) = Var(X) + Var(Y) + 2Cov(X,Y)\)

\(E(X^2) = 0.33 + 9\cdot0.17 = 1.86,\)

\(E(Y^2) = 25\cdot0.07 + 100\cdot0.03 = 4.75,\)

\(Var(X) = 1.86 - 0.84^2 = 1.1544,\)

\(Var(Y) = 4.75 - 0.65^2 = 4.3275,\)

\(Var(Z) = 1.1544 + 4.3275 + 2\cdot1.004 = 7.4899.\)